Extension spatio-temporelle du modèle chèvre INRA 2018 : 1. Application à l'alimentation en lots

Daniel SAUVANT; Patrick CHAPOUTOT; Sylvie GIGER-REVERDIN; Bertrand BLUET

doi:10.20870/productions-animales.2021.34.4.5354

Articles

Daniel SAUVANT, Patrick CHAPOUTOT, Sylvie GIGER-REVERDIN, Bertrand BLUET

Vol. 34 No 4 (2021) 305-326

Publié : 3 March 2022

DOI : https://doi.org/10.20870/productions-animales.2021.34.4.5354

Chapeau

Comme pour les autres espèces de ruminants, le modèle INRA 2018 a permis de mettre à jour les principes de l’alimentation pour un animal moyen. Mais en pratique, les chèvres sont généralement réparties en groupes par niveau de production et reçoivent des rations complètes distribuées seules ou avec un complément de fourrages à volonté. Cela a donc nécessité de d’étendre le modèle INRA 2018 à l’alimentation en lots des chèvres.

Introduction

Le modèle INRA 2018, issu du projet dit « Systali », s'est appuyé sur des actualisations de lois biologiques sous-jacentes pour établir les nouvelles valeurs du calcul des besoins alimentaires et des réponses des animaux ruminants à l'alimentation (figure 1, INRA, 2018). Cet ouvrage comprend le chapitre 21 consacré aux caprins (Sauvant et Giger-Reverdin, 2018), sachant que certains aspects concernant la nutrition et l'alimentation des chèvres sont traités dans d'autres chapitres de l’ouvrage (INRA, 2018) : lois de réponse (Ch. 9), rejets azotés (Ch. 13) et de méthane (Ch. 14), composition corporelle (Ch. 6), composition du lait (Ch. 11), acidose (Ch. 15). Dans le chapitre 21, qui représente l'essentiel du « modèle caprin INRA, 2018 », toutes les données de base des modèles de calculs des besoins et des réponses aux pratiques alimentaires ont été revisitées. Cependant, ces lois ne concernent qu'un individu « moyen » alors que les pratiques alimentaires des caprins s'appliquent essentiellement au niveau des lots d'animaux, c'est à dire à une échelle plus intégrée (figure 1). En outre, dans le chapitre 21, de nouveaux modèles d'évolutions dans le temps des principaux critères liés à la croissance, à la lactation, à la gestation et à la dynamique des réserves ont été proposés ; en revanche, ils n'ont pas été intégrés au sein d'un modèle global cohérent. Ces différents aspects ont été abordés de façon résumée par Sauvant et Bluet (2020).

Ce travail a donc été entrepris pour se rapprocher des pratiques des éleveurs en réalisant un élargissement spatio-temporel des recommandations caprines INRA 2018 (figure 1). Il a consisté à modéliser, d'une part, la problématique de l'alimentation en lots et, d'autre part, les articulations entre les principaux phénomènes dynamiques d'une chèvre moyenne sur un cycle de production. Seul le premier aspect est considéré dans cette première publication. Le second sera présenté dans la publication suivante (Sauvant et al., 2021). Toutes ces approches sont intégrées dans le logiciel INRATION®-Rumin'Al de calcul des rations des caprins.

Figure 1. Les niveaux d'échelles spatio-temporelles pris en compte en nutrition et alimentation des caprins.

Save View full size Expand inline Collapse inline

Les différents sigles utilisés dans cet article sont présentés dans le glossaire (encadré 1).

Encadré 1. Glossaire.

BalProRu : Balance Protéique du Rumen en g/kg MS

BesUFL : Besoins énergétiques en UFL/j

BesUFLgain : Besoins énergétiques liés à la croissance en UFL/j

BesUFLgest : Besoins énergétiques liés à la gestation en UFL/j

BilUFL : Bilan énergétique en UFL/j

bVECO : valeur minimale d'encombrement de l'aliment concentré en UEL/kg MS

CI : Capacité d'ingestion en UEL/j

CODPOT : Écart du potentiel de production de lait standard moyen du lot par rapport à 4 kg

CODPROP : Code caractérisant la proportion d'animaux ayant leurs besoins énergétiques couverts suite au choix de la cible

CODTRI : Code lié au niveau de refus

CODUEF : Code caractérisant l'impact de la qualité du fourrage sur sa valeur d'encombrement

COUV : Proportion d’animaux ayant leurs besoins énergétiques couverts

dMO : digestibilité de la matière organique en %

EffPDI : Efficience des PDI

Ind_CI_Gest: Indice correctif de la capacité d'ingestion lié au stade de gestation

Ind_CI_Lact : Indice correctif de la capacité d'ingestion lié au stade de lactation

Ind_CI_MAT: Indice correctif de la capacité d'ingestion lié à la teneur en MAT de la ration

MG : Production de Matières Grasses en g/j

ML : Production de lactose en g/j

MP : Production de Matières Protéiques en g/j

MSI : Matière Sèche Ingérée en kg/j

NDF : Teneur en paroi végétale (% MS)

NECst : Note sternale d'état corporel à la mise-bas

NO : Niveau relatif de l'offert par rapport à l'ingéré

PCO : Proportion de COncentré sur la base de la MS

PDI : Protéines Digestibles dans l'Intestin

PL : Production Laitière brute en kg/j

PLS : Production de Lait Standard (TB = 35 g/kg, TP = 31 g/kg), en kg/j

PV : Poids Vif en kg

PV^0,75: Poids métabolique en kg

RapCibLot : Rapport PLS potentielle de la chèvre cible/ PLS potentielle de la chèvre moyenne du lot

REDET : Coefficient de réduction de l'écart-type intra-lot des productions laitières

TB : Taux Butyreux en g/kg

TP : Taux Protéique en g/kg

TSg : Taux de Substitution global

TSm : Taux de Substitution marginal

UEL : Valeur d'encombrement en UEL/kg MS

UFL : Unité Fourragère Lait

UFLVPRpot : Variations Potentielles des Réserves corporelles en UFL/j

VE : Valeur d'Encombrement

Préfixe ou suffixe :

Att : Attendu

B : Coefficient de pente

Cib : Chèvre cible

CO : COncentré

COD : Code

Const : Constat

Corr : Corrigé

Ec : Écart

ET : Écart-Type

fix : Distribution en quantité fixe

FO : FOurrage

i : Quand il s'agit d'une valeur individuelle

max : Maximum

mél : Mélange

MG : Production de matières grasses

ML : Production de lactose

moy : Moyenne

MP : Production de Matières Protéiques

obs : Observé

P : Proportion

Pen : Pénalité

Piv : Pivot nutritionnel avec un bilan énergétique nul

pot : Potentiel

pot300 : Potentiel moyen sur la lactation entière (300 j)

Rép : Réponse

sup : Supplémentaire

T : Table

th : Théorique

tot : Total

1. La problématique de l'alimentation en lots

1.1. Définition du lot alimentaire et des animaux repères

Compte tenu des contraintes de conduite d’élevage, l'alimentation des chèvres ne peut se pratiquer à l'échelle des individus, mais elle s'applique à une échelle organisationnelle plus large qui est le lot (figure 1). Un lot (alimentaire) correspond à un groupe d’animaux qui reçoit la même ration au sens qualitatif. Cependant, les individus du lot ont tous des potentiels et des besoins différents liés à leurs propres caractéristiques : production laitière, âge, poids, stade de lactation, etc. Pour gérer au mieux la conduite alimentaire d'un lot, on prend en compte uniquement la variabilité des productions laitières, car elle est à la fois la plus facile à mesurer et la plus déterminante (voir plus loin). Ainsi, on repère systématiquement 3 animaux en fonction de leur production : la « chèvre moyenne », la « chèvre-cible » et la « chèvre faible productrice » correspondant au premier décile des productions (Idele, 2011). Cette approche était déjà appliquée dans le logiciel « Capalim » sur la base du modèle INRA, 2007. La ration commune (fourrages + concentrés) distribuée au lot est donc établie de façon à ce que la chèvre cible soit alimentée à son potentiel de production comme défini dans le système INRA, 2018. De fait, cette chèvre cible est la seule alimentée à son potentiel. Ainsi les autres chèvres, sont dans une situation de réponses, car elles sont, soit suralimentées (si leur potentiel est inférieur à celui de la cible), soit sous-alimentées (si leur potentiel est supérieur à celui de la cible). Cette notion d'animal cible est également pratiquée chez les brebis laitières (Bocquier et Caja, 2001). Le niveau de production de cet animal cible est défini de manière à ce qu'une proportion voulue des animaux ait ses besoins énergétiques couverts (0,75 par exemple correspond à une cible de 75 %). À titre d’exemple, la figure 2 montre, pour un lot produisant 4,23 ± 0,8 kg/j de PLS potentielle (PLSpot), la position de ces 3 chèvres par rapport à la distribution, selon une loi normale, des PLSpot c'est à dire ramenées à un lait avec un TB de 35 g/kg et un TP de 31 g/kg. La figure 2a présente l'histogramme de la distribution des PLSpot et la figure 2b la droite de Henry qui permet d'obtenir les PLSpot des 3 chèvres « faible », « moyenne » et « cible » (3,37, 4,24 et 4,68 kg/j respectivement) à partir des pourcentages des chèvres ayant leurs besoins énergétiques couverts (10, 50 et 75 %, respectivement). Ces 3 valeurs se calculent par l'application d'une fonction inverse de la loi normale.

Une fois ces animaux définis, toutes les chèvres du lot reçoivent la même quantité d'aliment concentré que la cible. On considère que chaque individu ingère cette quantité, sauf dans le cas d'une ration mélangée comprenant un fourrage et un concentré qui sera traité plus loin. L'ingestion de fourrage dépend alors de la capacité d'ingestion et de la substitution entre les concentrés et les fourrages autour de l'état d'équilibre énergétique (voir plus loin). La chèvre moyenne est importante à repérer, car elle est considérée comme ayant les caractéristiques moyennes du lot, notamment en termes d’ingestion de fourrage et permet ainsi de piloter la distribution. La chèvre faible productrice est utilisée comme « sentinelle » par rapport à certains risques nutritionnels (voir plus loin). Les réponses de production de l'ensemble du lot sont la somme des réponses des individus calculées à l'aide des équations de réponse INRA, 2018.

Figure 2. Illustration de la chèvre « cible », « moyenne » et « faible » : (a) Histogramme de répartition des productions laitières potentielles standards (PLSpot) et (b) détermination à l'aide de la droite de Henry des niveaux de PLSpot des chèvres moyenne (4,23), cible (4,68) et faible (3,37) à partir du pourcentage des animaux ayant leurs besoins UFL couverts et d'une fonction loi normale inverse.

Save View full size Expand inline Collapse inline

1.2. Les démarches appliquées

Plusieurs démarches sont appliquées pour raisonner l'alimentation des lots de chèvres :

i) Lorsqu'on connait les potentiels de production des individus (PLpot_i, TBpot_i, TPpot_i, PLSpot_i), il est possible de calculer les réponses multiples de production d'un lot en passant par le calcul des réponses individuelles observées (PL_i, TB_i, TP_i, PLS_i, figure 3) et en tenant compte de critères définissant le contexte d’alimentation du lot (proportion des animaux ayant les besoins couverts par le choix de la cible, qualité du fourrage, potentiel de production...). Cette démarche est décrite dans la partie 3 ;

ii) en revanche, mises à part les productions observées, le plus souvent on ne dispose pas d'information sur les potentiels productifs des animaux. Il convient alors de pouvoir mettre en œuvre une démarche, en quelque sorte réciproque de la précédente, de type « ingénierie reverse » permettant de calculer les productions potentielles à partir des données observées. Cette approche est présentée dans la partie 4 de cet article (figure 3).

Figure 3. Les démarches réciproques reliant les critères observés et potentiels des individus i au sein d'un lot.

Save View full size Expand inline Collapse inline

iii) Enfin, ces différentes approches peuvent être combinées à l'aide de deux principaux modes de calcul. (1) Le mode « calcul » permet d’explorer les situations possibles au sein d'un contexte. Dans ce mode, les quantités ingérées de chaque aliment seront déterminées par calcul pour nourrir l’animal cible à son potentiel et saturer la capacité d’ingestion de chaque individu. (2) Le mode « constat » permet quant à lui d’effectuer les démarches de calcul à partir des quantités moyennes d’aliments ingérées par le lot et données par l’utilisateur, telles qu’il les a constatées. Ces deux approches seront détaillées dans la partie 5 de cette publication.

1.3. Les informations connues a priori

Deux principales catégories de données et d'informations sont utilisées dans la gestion des lots :

i) la production laitière brute moyenne « observée » du lot au stade considéré (PLmoy, kg/j) ainsi que les données de production individuelle de lait brut (PL_i). Ces données permettent de quantifier la dispersion des individus autour de la PLmoy, appréciée par l'écart-type d'une distribution supposée gaussienne (ETPL) comme dans la figure 2. Si l’on ne peut pas faire l'hypothèse d'une loi normale de distribution des PLmoy il convient de diviser le lot de N chèvres en sous-lots de n_i chèvres (N = Σn_i) et de niveau de production PL_i (écart de 0,2 kg/j entre sous-lots). La même approche s'applique également pour les productions laitières standards PLS ;

$P L m o y = \frac{\sum_{i} n_{i} \times {P L}_{i}}{N}$

$E T P L = \sqrt{\frac{\sum_{i} [n_{i} \times {({P L}_{i} - P L m o y)}^{2}]}{(N - 1)}}$

ii) les estimations des potentiels moyens du lot à l’échelle de la lactation (production laitière potentielle à 300j, du TB potentiel moyen de la lactation, du TP potentiel moyen de la lactation, soit respectivement PLpot300, TBpot300 et TPpot300), dont on peut déduire les productions potentielles brutes (PLpot), ainsi que les TBpot et TPpot au stade considéré, grâce aux équations 21.1a, 21.1b et 21.2 du chapitre 21 (INRA, 2018). De ces valeurs, on peut déduire la PL standard potentielle au même stade (PLSpot) :

$P L S p o t = \frac{P L p o t}{0,389} \times [0,389 + 0,0052 \times (T B p o t - 35) + 0,0029 \times (T P p o t - 31)]$
[1]

Au-delà de ces données liées à la production, d'autres caractéristiques utiles concernant l’alimentation d’un lot sont à prendre en compte. Il s'agit en particulier de son stade moyen de lactation et/ou de gestation, du poids et de la parité des animaux. Sur ces aspects, pour des raisons pratiques, on considérera dans l’approche que chaque individu i possède les caractéristiques de la moyenne du lot. Il convient également de prendre en compte la nature, la composition et la valeur alimentaire des aliments offerts, en tenant compte des interactions digestives, et le niveau de refus des fourrages.

2. Rappels et actualisations des principales équations de base

En pratique, cette démarche a été conçue et mise en place en plusieurs étapes principales. Un premier travail a consisté à modéliser l'influence du niveau de refus d'un fourrage sur son ingéré et à actualiser les lois de réponse aux apports d'aliments concentrés qui avaient été présentées dans INRA 2018. Au préalable, il est utile de rappeler les deux principales équations appliquées pour prédire les capacités d'ingestion et les besoins en énergie des animaux en lots qui sont les 2 principaux paramètres sur lesquels s’appuie le calcul des niveaux d’ingestion de fourrages et de concentrés.

2.1. Rappels sur la prévision de la capacité d'ingestion et des besoins énergétiques individuels.

Ces deux critères sont essentiels dans les approches de l'alimentation des lots. La construction des équations de prévision correspondantes a été présentée par Sauvant et Giger-Reverdin (2018).

Le calcul de la capacité d'Ingestion des individus (CI_i, en UEL/j) est fonction du poids vif moyen du lot (PV) et de leur production laitière standard potentielle (PLSpot_i, cf. Eq 21.46, INRA, 2018). Il intègre également des indices multiplicatifs, compris entre 0 et 1, pour tenir compte des stades moyens de lactation (Ind_CI_Lact), de gestation (Ind_CI_Gest) du lot et de la teneur en MAT du régime (Ind_CI_MAT), ce dernier point nécessitant un calcul itératif.

${C I}_{i} = [1, 3 + 0, 016 \times (P V - 60) + 0, 24 \times {P L S p o t}_{i}]$

$\times {I n d_C I}_{L a c t} \times {I n d_C I}_{G e s t} \times {I n d_C I}_{M A T}$
[2a]

La question de l'influence du niveau de la quantité offerte sur la CI sera abordée dans l'encadré 2. Pour les calculs, on retient en général une hypothèse de PV identique pour tous les animaux, correspondant au PV moyen du lot. Pour information, l'écart-type inter-chèvres du PV varie en général entre 8 et 12 kg au sein d'un lot, ce qui correspond à une variabilité de la CI de 0,13 à 0,19 UEL/j, cette variabilité est négligée dans les calculs.

Par ailleurs, un travail (Sauvant, Giger-Reverdin, Delagarde, non publié) de comparaison des niveaux de Matière Sèche Ingérée (MSI) a été effectué entre trois grandes séries de données mesurées : (1) la base Caprinut (INRA, 2018) qui a servi à établir l'Eq [2a], (2) la base de données expérimentales d'ingestion de l'Unité MoSAR (Giger-Reverdin et al., non publié) et (3) la base de données expérimentales d'ingestion de Méjussaume (Unité Pegase, Delagarde et al., non publié). Il apparaît que les résultats de MSI sont très cohérents entre les trois bases de données lorsque les valeurs de MSI sont corrigées par le niveau de production de lait et le PV pris comme covariables. En outre, ils ne diffèrent pas des résultats obtenus lorsqu'on applique à ces données huit équations publiées dans la bibliographie de prévision de la MSI des chèvres laitières. Ces différents résultats renforcent le bien-fondé de l'Eq [2a].

Le calcul des besoins énergétiques théoriques des individus (BesUFLth_i, en UFL/j) se fait à partir de l'équation suivante, sachant que le programme INRATION®/Rumin’Al tient compte aussi des besoins de croissance (BesUFLgain) et de gestation (BesUFLgest) tels qu'ils sont formulés dans le chapitre 21 (INRA, 2018) :

${B e s U F L t h}_{i} = 0,389 \times {P L S p o t}_{i} + 0,0406 \times {P V}^{0,75} - {U F L V P R p o t}_{i}$
[2b]

Le critère UFLVPRpot traduit la dynamique des réserves énergétiques qui est liée au potentiel de production, au stade dans le cycle de production et à la note sternale d'état corporel moyen du lot à la mise bas (NECst). Son calcul est décrit dans l’équation 21.19 du chapitre 21 (INRA, 2018). Ainsi lorsque UFLVPRpot est supérieur à 0, les animaux mobilisent de l'énergie qui vient s'ajouter aux apports. Cette prise en compte de la dynamique des réserves est nécessaire puisque les lois de réponses multiples aux apports (cf. Matériel Supplémentaire) s'appliquent à partir du pivot nutritionnel de chaque chèvre pour un bilan énergétique théorique équilibré :

${B i l U F L t h}_{i} = {U F L i n g é r é e s}_{i} - {B e s U F L t h}_{i} = 0$

2.2. Actualisation des équations de prévision des réponses individuelles aux apports alimentaires

a. Influences des niveaux offerts et des apports de concentré

Depuis la publication des équations INRA 2018, de nouveaux résultats ont été obtenus ce qui nous a amenés à actualiser nos propositions. Celles-ci concernent, d'une part, les réponses de l’ingestion aux variations de l’offre en fourrages et du niveau des refus (encadré 2) et, d'autre part, les réponses multiples aux apports d'aliments concentrés qui ont été actualisées grâce à la prise en compte de nouvelles données (voir Matériel Supplémentaire).

Encadré 2. La modélisation des influences des niveaux de fourrages offerts et des refus.

L’influence du niveau d’offre et de tri des fourrages sur le niveau d’ingestion n'avait pas été abordé dans INRA (2018). Pour gagner en précision, nous avons cherché à en intégrer les effets sur la capacité d'ingestion et sur la valeur UEL des fourrages des animaux. Ainsi, nous avons rassemblé les données de 7 expériences publiées dans lesquelles le niveau du fourrage offert avait varié entre les 2 lots d'une même expérience (l'une d'elles comportant 3 lots). La relation intra-expérience moyenne obtenue est assez précise. Elle correspond à la régression suivante avec les niveaux d'ingestion de MS exprimés en g de MSI par kg de PV métabolique (PV^0,75) pour rendre comparables les données entre les différentes expériences :

$M S I n g é r é e / {P V}^{0.75} = 57, 14 + 0, 240 \times M S o f f e r t e / {P V}^{0.75}$
(n=15, nexp=7, ETR=3.2) [E1]

Il convient de noter que cette prise en compte de la réponse de l'ingestion à l'offre de fourrage intègre en réalité deux phénomènes : d'une part, la stimulation de l’appétit par une offre supérieure et, d'autre part, le tri effectué par les animaux qui induit une baisse de la teneur en parois du fourrage ingéré comparativement à l'offert et donc une plus faible valeur UELFO. Selon le coefficient de pente de cette régression [E1], lorsqu'on offre 100 g de MS de fourrage en plus, son ingestion augmente de 24±4 g MS, la différence, soit 76 g, correspondant à des refus. Logiquement, le niveau des refus s'accroît systématiquement avec celui de l'offre. Au sein de ces expériences, les niveaux moyens de refus par rapport à l’offert ont été de 18,1 et 39,4 % en MS, respectivement pour les lots « bas niveau » et « haut niveau » d'offre. Pour prendre en compte ces résultats, pour un animal caractérisé par sa CI et selon les valeurs d'encombrement (UELFO) des fourrages dans les tables INRA 2018 (T), on considère qu’on a un niveau maximal d'ingestion de fourrage de MSIFOmaxT= CI/UELFO. Si on lui offre une quantité supplémentaire de fourrage ΔMSFOsup, l’effet de stimulation de l’appétit conduit à accroître son ingestion selon la relation :

$M S I F O m a x = M S I F O m a x T + 0, 24 \times M S F O s u p$
[E2]

La proportion de MSFO de refus (0
$R = \frac{0, 76 \times M S F O s u p}{M S I F O m a x T + M S F O s u p}$
[E3]

d’où on déduit une première expression de MSIFOmaxT :

$M S I F O m a x T = - M S F O s u p + \frac{(0, 76 \times M S F O s u p)}{R}$
[E4]

D’autre part, le niveau relatif d'offert de MS (NO) par rapport à l'ingéré des tables INRA 2018 est :

$N O = \frac{M S I F O m a x T + M S F O s u p}{M S I F O m a x T}$
[E5]

Par ailleurs, ce ratio est le même s'il est exprimé en CI, on en déduit donc une seconde expression de MSIFOmaxT :

$M S I F O m a x T = \frac{M S F O s u p}{N O - 1}$
[E5’]

Des deux expressions [E4] et [E5’] de MSIFOmaxT, on déduit :

$\frac{M S F O s u p}{N O - 1} = - M S F O s u p + (\frac{0, 76 \times M S F O s u p}{R})$
[E6]

On en déduit une relation entre les niveaux relatifs de l'offert (NO) et de refus (R) :

$N O = \frac{0,76}{0,76 - R}$
ou bien $R = \frac{0,76 \times (N O - 1)}{N O}$ [E7] et [E7']

Cette double relation symétrique permet de prédire NO en fonction de R et réciproquement, en fonction de ce qu'on recherche. Lorsque R=0, on est en situation semi-limitée (ou « sub ad libitum ») ce qui ne correspond pas au contexte d'application du système des UEL. Dans le système des UEL, on admet le principe qu'il y a en pratique 5 % de refus (R=0,05), donc une offre moyenne NO=1,0704. En pratique, trois situations de base sont considérées pour évaluer les influences du niveau de l'offert et du tri sur l'ingestion et la valeur nutritive du fourrage considéré. Pour cela, une variable CODTRI distinguée par 3 niveaux (0, 1 ou 2) a été créée. La situation CODTRI = 0 correspond à un niveau moyen de refus d'environ 5 %, c'est la situation moyenne qui correspond aux valeurs UEL et des UFL des fourrages dans les tables INRA (tableau E1). Les valeurs CODTRI = 1 et 2 correspondent aux niveaux de refus d'environ 15 et 25 % respectivement, on peut également envisager d'utiliser des demi-niveaux de CODTRI soit 0,5 et 1,5 ou des valeurs > 2 si les refus excèdent 25 %. En pratique, on considère a priori que les éleveurs travaillent avec un niveau de refus de 10 % (R = 0,1), ce qui revient à multiplier la CI par un coefficient de 1,080 (Eq 9, et tableau E1). Les relations entre les 3 critères, NO, %Refus et CODTRI, sont assez simples et permettent d'envisager de les appliquer en fonction du contexte d'élevage considéré puisqu'on a approximativement :

$% R e f u s = 5 + 10 \times C O D T R I$
[E8]

Ceci permet d'appliquer ce principe dans le calcul des rations en distinguant 3 niveaux majeurs de CODTRI (0/1/2) et le cas échéant des niveaux intermédiaires, si on dispose de données assez précises pour le faire.

Cependant, l'approche ci-dessus ne concerne que la partie fourragère de la ration. Ainsi, pour le calcul, le coefficient NO et le facteur multiplicatif du tableau 1 ne doivent donc s'appliquer qu’à la fraction de l’encombrement qui correspond à l’ingestion de fourrages. Il est donc logique que l'effet du NO sur la CI, conduisant à la CI corrigée (CIcorr), soit modulé par la proportion de concentré PCO de la ration qui n'induit pas de refus, on a donc :

$C I c o r r = C I i n r a \times [1 + (N O - 1, 0704) \times (1 - P C O)]$
[E9]

Par exemple, à partir de la CIinra (Eq [2a] ou Eq 21.46 de INRA 2018) qui suppose CODTRI=0 et 5 % de refus, dans le cas d’une ration avec un refus moyen de 10 %, la CI corrigée des animaux sera CIcorr = 1,080*CIinra si PCO = 0, par contre, si PCO = 0,25, on aura CIcorr = 1,060*CIinra et si PCO = 0,5, on aura CIcorr = 1,040*CIinra etc.

Selon des résultats récents non publiés obtenus par Giger-Reverdin (UMR MoSAR) à partir de nombreux essais, si on admet que la valeur UELFO des tables correspond à CODTRI = 0, lorsque CODTRI = 1 et 2 la baisse d'encombrement est de 0,02 et 0,04 UEL/kg MS respectivement.

Enfin, il est également nécessaire de tenir compte de l'influence positive du tri sur les valeurs UFL et PDI de ces fourrages. Nous avons appliqué les modifications observées en moyenne par Giger-Reverdin et al. (non publié) sur 331 résultats de mesure des compositions des fourrages offerts et effectivement ingérés. Comme pour l’encombrement, on considère que les valeurs UFL des tables INRA correspondent à CODTRI=0. Ainsi, dans le tableau E1, les effets sur la dMO et la valeur UFL du fourrage ont été ajoutées pour permettre d'entrer ces valeurs dans le moteur de calcul. Ces modifications sont intégrées dans les différents calculs faisant intervenir les niveaux d'ingestion.

b. Les réponses aux apports d'aliment concentré ou de nutriments à partir des situations de pivot nutritionnel BilUFLth = 0

Dans la démarche de calcul (cf. partie 3.1), il convient de calculer les rations théoriques équilibrées en énergie au pivot nutritionnel de chaque individu. Une fois que les calculs des pivots individuels sont réalisés, il est possible d'appliquer deux types de lois de réponses des productions de matières grasses, de protéines et de lactose (RepMG, RepMP et RepML respectivement) :

i) les réponses aux apports de concentré ΔMSICO autour de BilUFLth=0 (voir Matériel Supplémentaire) ou bien, lorsque les pivots sont calculés à la fois pour BilUFLth=0 et EffPDI=0,67 ;

ii) les réponses aux écarts d'apports de nutriments ΔUFL et ΔPDI qui ont été présentées dans les équations 21.55 à 21.58 du chapitre 21 du LR (INRA, 2018).

À partir des trois réponses de MG, MP et ML on peut calculer la réponse de la PLS avec une équation semblable à l’équation [S4h] (voir Matériel Supplémentaire n°1). Lorsqu'elles sont appliquées à un même jeu de données, les réponses aux ΔUFL sont très comparables aux réponses obtenues avec les concentrés. En revanche, les réponses aux ΔPDI peuvent être différentes en cas d'apport protéique élevé ou faible par rapport aux besoins, en fonction notamment de la valeur azotée du concentré. Pour chaque situation considérée, il est donc recommandé d'examiner les deux familles de réponses : les réponses aux concentrés présentent l'intérêt de s'appuyer sur l'apport de concentré, critère concret ayant un coût qui doit être connu pour une bonne gestion et utilisation optimale de ces aliments, et les réponses aux nutriments qui peuvent compléter l'analyse des réponses sur le volet protéique.

c. Cas particulier des rations comprenant des fourrages et concentrés mélangés

Dans le cas d'une ration comprenant des fourrages et concentrés mélangés, la démarche consiste également à établir la ration du lot de sorte que l’animal cible soit nourri à son potentiel. On considère dans ce cas que chaque individu ingère l’ensemble du mélange (proportion fixe de concentré) au prorata de sa capacité d’ingestion. Avec ce mode d'alimentation, une fois que les calculs des pivots individuels sont réalisés (partie 3.1) et que la chèvre cible est choisie (partie 3.2.1), il est possible d'appliquer les lois de réponses des productions de MG, MP et ML aux écarts ΔPCO (PCO de la ration distribuée – PCO pivot de l’individu) avec les équations présentées au tableau 21.10 du chapitre 21 (INRA, 2018). La question des rations semi-complètes est traitée plus loin. Les lois de réponses aux apports de PDI et UFL ne sont pas considérées dans ce dernier cas.

3. Modélisation des réponses des lots à partir des potentiels individuels

Cette partie, évoquée brièvement plus haut (cf. 1.2), est conduite en trois étapes. La première consiste à calculer, pour chaque individu considéré à son potentiel, la ration qui permet d'atteindre le pivot nutritionnel, c'est à dire un bilan BilUFLth = 0. La deuxième consiste à identifier l'animal cible, puis à calculer sa ration et la troisième, à en déduire les réponses individuelles des autres chèvres du lot qui se verront proposer la ration de la cible.

3.1. Étape 1 : le calcul des rations individuelles équilibrées au « pivot nutritionnel »

a. Principes de base du calcul

Dans cette étape, on recherche pour chaque animal les valeurs des niveaux d’ingestion individuels en fourrages et concentrés (MSIFOPiv, MSICOPiv, kg/j) de la ration pivot, c’est-à-dire équilibrée pour l’énergie, tout en intégrant les interactions digestives et en saturant la CI. Les valeurs de ces niveaux d'ingestion individuels de la ration pivot (BilUFLth = 0) peuvent être obtenues simplement avec un système de 2 équations (énergie et encombrement) à 2 inconnues (MSIFO, MSICO). Si une partie du fourrage est distribuée en quantité fixe (MSIFOfix, kg/j), qui peut être par exemple un fourrage très palatable et rationné, il est nécessaire de tenir compte de son apport d'énergie (MSIFOfix x UFLFOfix) et de sa contribution à l'encombrement de la ration (MSIFOfix x UELFOfix). Le système des 2 équations à 2 inconnues s'écrit alors de la façon suivante :

$M S I F O \times U F L F O + M S I C O \times U F L C O = B e s U F L t h - (M S I F O f i x \times U F L F O f i x)$
[3]

$M S I F O \times U E L F O + M S I C O \times U E L C O = C I - (M S I F O f i x \times U E L F O f i x)$
[3’]

Dans ces deux équations MSIFO, UELFO et UFLFO représentent les critères liés au fourrage distribué ad libitum et MSIFOfix, UELFOfix et UFLFOfix ceux liés au fourrage distribué en quantité fixe à tous les animaux. Le concentré est caractérisé par ses valeurs UFLCO et UELCO. Rappelons que les valeurs UFL sont modifiées par les interactions digestives, ce qui nécessite un calcul itératif supplémentaire.

En pratique, on s'appuie sur la relation UELCO = TSg × UELFO, le taux de substitution globale TSg étant déterminé en fonction de MSICO par l'Eq [S1c] (voir Matériel Supplémentaire). Étant donné que UELCO dépend de TSg, qui dépend lui-même de MSICO la solution du système, il est nécessaire d'appliquer un calcul itératif initialisé par UELCO = bVECO qui est indiqué dans la table INRA 2018 (Ch. 25). D'une façon générale, après quelques itérations de calculs on obtient des solutions stables pour les quantités de MSIFO et MSICO au pivot, soit MSIFOPiv et MSICOPiv respectivement. La solution algébrique de ce système (méthode des déterminants) correspond aux niveaux d'ingestion recherchés au pivot nutritionnel :

$M S I F O P i v = \frac{⌊(C I - (M S I F O f i x \times U E L F O f i x) \times U F L C O) - (B e s U F L t h - (M S I F O f i x \times U F L F O f i x)) \times U E L C O⌋}{(U E L F O \times U F L C O - U F L F O \times U E L C O)}$
[4]

$M S I C O P i v = \frac{⌊(B e s U F L t h - (M S I F O f i x \times U F L F O f i x) \times U E L F O) - (C I - (M S I F O f i x \times U E L F O f i x)) \times U F L F O⌋}{(U E L F O \times U F L C O - U F L F O \times U E L C O)}$
[4']

S’il n’y a pas de solution algébrique réaliste au système, la solution pratique est décrite plus loin dans la partie 3.1.c.

Ces équations [4] et [4'] permettent de calculer la quantité de MS totale ingérée (MSItot) de chaque individu à son potentiel (MSItotPiv = MSIFOPiv + MSICOPiv + MSIFOfix). La figure 5a présente un exemple de calcul selon cette méthode des rations pivots pour chaque individu d'un lot. Sur cette figure 5a, nous avons indiqué les valeurs de MSIFOMaxT (= CI/UELFO = quantité de fourrage ad lib ingéré pour saturer la capacité d’ingestion s'il est apporté sans concentrés) de manière à pouvoir se rendre compte de l'écart important qui peut séparer ces valeurs de celles de MSIFOPiv pour les chèvres les plus productives. Cette approche peut s'appliquer par exemple lorsqu'on utilise un distributeur automatique individuel de concentré (ou DAC), sachant que dans ce cas l'éleveur constitue souvent des sous-lots alimentaires.

Dans le cas des rations comprenant des fourrages et concentrés mélangés, on utilise également cette approche, mais dans ce cas on doit calculer au préalable les teneurs en UFL et UEL du mélange (UFLmel et UELmel). La valeur UFLmel est la somme pondérée par la proportion de concentré du mélange (PCOmel) des teneurs en UFL du fourrage et du concentré :

$U F L m e l = U F L F O \times (1 - P C O m e l) + U F L C O \times P C O m e l$
[5]

Pour la valeur d'encombrement du mélange on propose d'appliquer l'équation suivante :

$U E L m e l = U E L F O \times (1 - P C O m e l)$

$+ U E L F O \times [0,6 + (b V E C O - 0,3) + 0,15 x P C O m e l] \times P C O m e l$
[5']

Dans cette équation, si bVECO = 0,3 (valeur moyenne la plus fréquente), on suppose que la valeur UELCO = 0,6 lorsque PCOmel = 0 et UELFO = 1 et UELCO = 0,75 lorsque PCOmel = 1 (et UELFO = 1). Lorsque bVECO s'écarte de la valeur 0,3, la différence bVECO-0,3 se répercute sur la valeur UELCO. Ces valeurs résultent de valeurs moyennes observées sur la base Caprinut (INRA, 2018). Ensuite, les Eq [3] et [3'] sont appliquées avec les valeurs UFLmel et UELmel du mélange (qui peut éventuellement être apporté en quantité fixe, un autre fourrage étant distribué ad libitum).

b. La prise en compte des modifications de la capacité d'ingestion et des valeurs alimentaires

D'une part, la capacité d'ingestion CI utilisée dans ces équations [3 & 3'] et [4 & 4'] correspond à l'application de l'équation CI INRA de base (Eq [2]) qui intègre les effets du stade lactation et de gestation, et la teneur en MAT du régime, modulée de l’effet du niveau de l’offre et du tri associé (qui lui-même dépend de la PCO de la ration, cf. tableau E1, encadré 2). L'intégration de ces aspects nécessite d'effectuer une boucle calculatoire supplémentaire pour résoudre le système des équations [3] et [3'], cependant celle-ci peut être combinée à la boucle calculatoire autour de MSICO et UELCO décrite ci-dessus.

D'autre part, étant donné qu'au cours des calculs les niveaux d'ingestion des aliments varient d'un animal à l'autre, ou d’une situation à l’autre pour un même animal, il importe de tenir compte des phénomènes d'interactions digestives (cf. Ch. 3, INRA, 2018). Donc, outre l'influence des variations du niveau d'ingestion (cf. Eq. 3.4, INRA, 2018), il est nécessaire de tenir compte des variations du critère BalProRu (cf. Eq 3.9, INRA, 2018) d'un animal à l'autre, sachant qu'il n'y a pas d'interactions liées au concentré chez la chèvre. Ceci est réalisé à travers un calcul itératif.

c. Cas particuliers des situations de solutions impossibles du système des équations [3] et [3']

Il arrive que le système des équations [3] et [3'] ne présente pas de solution positive pour MSIFOPiv et/ou MSICOPiv. Cette situation s'observe dans deux cas : (1) lorsque l'apport d'un fourrage seul de bonne qualité peut couvrir les besoins en énergie d'un animal tout en saturant sa CI, ou bien (2) à l'inverse, si on offre un mauvais fourrage à des animaux forts producteurs.

En pratique, dans le premier cas, qui concerne plutôt les animaux les moins producteurs d'un lot et qui conduit à une solution MSICOPiv < 0, on fixe alors MSICOPiv = 0 et l'ingestion de fourrage est alors MSIFOMaxT = CI/UELFO. En conséquence de cette situation, pour calculer ensuite les réponses de ces animaux, on applique les équations INRA de réponse à MSICO [S2a] à [S2f] (cf. Matériel supplémentaire), calculées à partir de MSICOPiv = 0, en considérant que l'apport de concentré est celui de la chèvre cible, soit MSICOCib.

La seconde situation, avec une solution MSIFOPiv < 0, s'observe sur les animaux fort producteurs d'un lot qui reçoivent un fourrage de qualité insuffisante, c'est à dire présentant une densité énergétique (DE=UFLFO/UELFO) trop faible, obligeant ainsi à un apport très conséquent de concentré. En pratique, il n'y a pas de solution et il est a priori nécessaire de reprendre le travail à son début en modifiant le contexte. Pourtant, bien que cela ne concerne qu’une très faible proportion du lot, il est fréquent que quelques individus soient dans cette situation et il est donc nécessaire de proposer une solution pour permettre le calcul à l’échelle de l’ensemble du lot. Compte tenu du fait que UELFO, UFLFO et UFLCO sont des valeurs peu variables, mais modifiées par les interactions digestives, on peut considérer que le problème résulte du fait que l'encombrement du concentré (ou le coefficient de substitution TSg) est trop élevé. Dans ce cas, compte tenu du fait qu'il y a une incertitude assez large sur ce paramètre, on propose de continuer le calcul en fixant un minimum de MSIFO = 0,1 kg MS/j et en résolvant l'équation [3] pour l'énergie afin d'obtenir la solution MSICO permettant de couvrir les besoins en UFL :

$M S I C O = \frac{(B e s U F L - 0,1 \times U F L F O)}{U F L C O}$
[6]

Puis on estime la valeur correspondante de UELCO à partir de l'équation :

$U E L C O = \frac{(C I - 0,1 \times U E L F O)}{M S I C O}$
[6']

Le calcul étant effectué sur un ensemble de 500 individus virtuels, il importe de repérer la proportion des situations anormales de ce type, sachant, d'après nos explorations, qu’elles ne doivent pas excéder 5-10 % des données pour éviter de biaiser le résultat final de la moyenne du lot.

3.2. Étape 2 : le repérage de la chèvre cible et le calcul de sa ration

Le calcul des réponses des lots à partir des potentiels individuels doit prendre en compte précisément le levier majeur de la gestion alimentaire des lots qui est la chèvre cible, le seul animal du lot à rester en situation de pivot nutritionnel, c'est à dire alimenté à son potentiel. Donc, pour cette chèvre les quantités de MSICOPiv et MSIFOPiv restent constantes. Les figures 2a et 2b montrent l'exemple d'un lot avec une cible couvrant les besoins UFL pour 75 % des individus. Le choix de la cible se fait selon la proportion des animaux ayant leurs besoins UFL potentiels couverts par la ration distribuée. Les lignes qui suivent présentent une méthode de calcul simple de la production de la cible en fonction notamment de la proportion des animaux ayant leurs besoins UFL couverts.

a. Prévision de la PLS potentielle de la « chèvre cible »

Rappelons qu'on suppose dans cette partie que les potentiels individuels des animaux sont connus. Il s'agit du potentiel moyen de production de lait brut (PLpot_i, kg/j), ainsi que TBpot_i et TPpot_i (g/kg), permettant de déduire la PLSpot_i et la dispersion des individus autour de cette moyenne, appréciée par une estimation a priori de son écart-type (ETPLSpot). Pour déterminer PLSpot de la chèvre cible, qui dépend des caractéristiques du lot (PLSpotmoy, ETPLSpot) et de la proportion (choisie par l’éleveur) des individus qui verront leurs besoins UFL couverts, on cherche à prédire d'une façon simple le rapport RapCibLot entre les niveaux de PLS potentielles de la chèvre cible (PLSpotcib) et de la chèvre moyenne du lot (PLSpotmoy).

Pour construire l'équation de prévision de RapCibLot, nous avons simulé les effets sur cette variable de la combinaison factorielle des trois facteurs les plus influents suivants :

i) La proportion d'individus ayant les besoins UFL couverts suite au choix de la cible. Six proportions ont été testées : 0,20 ; 0,50 ; 0,66 ; 0,75 ; 0,85 ; 0,95. Pour simplifier les calculs, ces valeurs ont été transformées en niveaux par rapport à la valeur de 0,50 (soit CODPROP = -0,30 ; 0,0 ; 0,16 ; 0,25 ; 0,35 ; 0,45) ;

ii) le potentiel de production moyen du lot. Sept valeurs de PLSpot ont été testées : 2,0 ; 2,5 ; 3,0 ; 3,5 ; 4,0 ; 4,5 et 5,0 kg/j. Elles ont été transformées en un code écart à la valeur de 4 kg /j, soit CODPOT = -2,0 ; -1,5 ; -1,0 ; -0,5 ; 0,0 ; 0,5 ; 1,0 kg/j ;

iii) l’écart-type intra-lot de la PLSpot (ETPLSpot). Trois valeurs ont été testées : 0,5 ; 0,8 ; 1,1 kg PLSpot/j.

Ces 126 combinaisons des 3 facteurs ont été réalisées de manière à ce que les 3 variables codantes correspondantes ne soient pas corrélées entre elles. Elles définissent la zone de validité de la prédiction, avec en particulier -0,30≤CODPROP≤0,45. La prise en compte des influences de ces 3 facteurs sur RapCibLot, représentés par les variables CODPROP, CODPOT et ETPLSpot, a été faite par une régression multiple :

$R a p C i b L o t = 0,8587 + 0,5651 \times C O D P R O P + 0,4708 \times {C O D P R O P}^{2}$

$- 0,1819 \times C O D P R O P \times C O D P O T$

$+ 0,1429 \times E T P L S p o t$
(n=126, R² = 0,93, ETR=0,053) [7]

D'après cette régression très significative, le critère RapCibLot augmente de façon linéaire lorsque ETPLSpot s'accroit, en revanche l'effet positif de CODPROP est curvilinéaire, de plus il y a un effet d'interaction négatif très significatif entre CODPROP et CODPOT. Il traduit le fait que l'influence de PROP sur RapCibLot est moins marquée lorsque le potentiel de production est plus élevé comme l'illustre la figure 4.

Figure 4. Réponse du critère RapCibLot en fonction du % d'animaux ayant leurs besoins UFL couverts au niveau de la chèvre cible et du potentiel moyen du lot (PLSpot).

Save View full size Expand inline Collapse inline

Par exemple, pour un lot ayant un potentiel de 3,5 kg PLSpot (CODPOT = -0,5kg) avec un ETPLSpot de 0,9 kg PLS et avec un objectif de 75 % des animaux ayant leur besoin en UFL couvert (soit CODPROP=0,25) on a :

RapCibLot = 0,8749 + 0,2036 x 0,25 + 1,205 x 0,25² - 0,1684 x 0,25 x (-0,5) + 0,1572 x 0,9 = 1,164

Dans ce cas, l'animal cible produit PLSpotCib = PLSpotmoy x RapCibLot = 3,5 x 1,164 = 4,07 kg/j.

Nous pouvons ainsi conclure :

i) qu’il est possible de prédire avec une précision assez satisfaisante le rapport de PLSpot de la chèvre cible à la moyenne du lot en fonction de 3 critères (1) l'objectif de proportion d'animaux aux besoins UFL couverts par le choix de la cible (2) l'écart type de la PLS intra-lot et (3) le potentiel de production du lot ;

ii) qu’un problème soulevé par cette équation concerne le fait que le critère ETPLSpot n'est pas toujours connu puisqu'il résulte des potentiels individuels qu'on peut être amené à rechercher (cf. partie 4). Dans ce cas, il est nécessaire de proposer une estimation initiale réaliste (à dire d'expert) à partir des données observées (0,8 par exemple, cf. partie 4) pour initier la boucle de calculs des quantités ingérées et des réponses jusqu’à convergence vers la valeur stabilisée (cf. la partie 5 et la figure 8) ;

iii) que dans certaines situations, on peut être amené à vouloir appliquer la démarche réciproque, c'est à dire prédire le % d'animaux ayant leurs besoins couverts par la cible en fonction des valeurs de RapCibLot, ETPLSpot et du potentiel PLSpotmoy. Nous avons calculé cette équation à partir d'un ensemble de données simulées au sein des étendues suivantes : 0,5

Enfin, à partir de l’estimation de RapCiblot, il est alors possible de calculer le % d’animaux dont les besoins sont couverts :

$% A n i m B e s c o u v e r t s = - 61,89 - 23,56 \times E T P L S p o t$

$+ 121,66 \times R a p C i b l o t + 4,489 \times P L S p o t m o y$
[7']

b. Détermination de l'apport de concentré à la chèvre cible

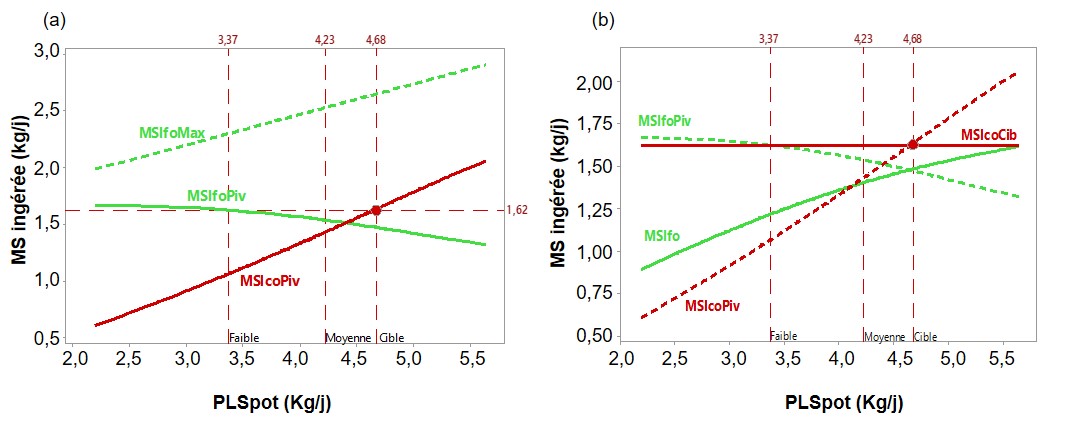
À la fin des calculs présentés en partie 3.1, on obtient les niveaux d'ingestion de MSIFOPiv et MSICOPiv (et éventuellement MSIFOfix) des pivots énergétiques individuels, correspondant à BilUFLth = 0, pour chacun des animaux du lot (ou des sous-groupes homogènes prédéterminés). Une fois que le niveau de PLSpot de la cible a été fixé (PLSpotCib, cf. partie 3.2.a), on ajuste une régression de degré 3 de MSICOPiv sur PLSpot sur l'ensemble des animaux (MSICOPiv = f(PLSpot)], comme l’illustre la relation en rouge sur la figure 5a. Connaissant la valeur de PLSpotCib, on obtient ainsi la valeur de MSICOCib qui correspond à MSICOPiv de l’animal cible et qui est distribuée identiquement à toutes les chèvres du lot (figure 5b). Cette modification (de la courbe pointillée rouge à la droite continue rouge de la figure 5b) va induire des réponses individuelles d’ingestion et de production (cf. partie 3.3). Les figures 5a et 5b résument cette démarche pour l'exemple de la figure 2 avec PLSpot moyen = 4,23 kg/j, PLSpotCib = 4,68 kg/j, UELFO = 1,05, UFLFO = 0,66, UFLCO = 1,05 et bVECO = 0,3. Dans cet exemple, on a MSICOCib = 1,62 kg/j.

Figure 5. (a) Exemple de calcul des ingestions de MS du fourrage à volonté (MSIFOPiv) et du concentré (MSICOPiv) en situation de pivot nutritionnel des individus selon leur potentiel de production (PLSpot) et (b) placement de la cible et de MSICOCib = 1,62, puis calcul des réponses individuelles de MSIFO.

Save View full size Expand inline Collapse inline

c. Optimisation du calcul de la ration de la chèvre cible

Le calcul de la ration de la chèvre cible à son niveau de PLSpot se fait en même temps que ceux de l'ensemble des chèvres du lot à l'aide du système des équations [3 & 3']. Cependant, il est aussi possible d'utiliser un processus d'optimisation plus large, inclus dans INRATION®V5, permettant, non seulement la couverture des besoins UFLth et la saturation de la CI, mais également la couverture adéquate de l'ensemble des autres besoins de cet animal (PDI, Minéraux...) ainsi que des critères nutritionnels recherché (BalProRu, teneur en NDF de fourrage...). Cette approche, développée par Faverdin (non publié) pour les vaches laitières, met en jeu une fonction d'optimisation technique à minimiser et basée sur l'addition de cinq fonctions de pénalités (écarts entre les performances permises par la ration et les objectifs de rationnement), de poids variable en fonction des critères considérés ; dans le cas des chèvres laitières, 5 critères sont retenus, avec les poids respectifs suivants :

i) pénalité pour des écarts par rapport à la production potentielle :

$P e n E c P L S = 50 \times {(P L S - P L S p o t)}^{2}$

ii) pénalité pour des écarts au bilan UFLth :

$P e n E c B i l U F L = 50 \times {B i l U F L t h}^{2}$

iii) pénalité pour des valeurs élevées ou faibles de BalProRu :

$P e n E c B P R = \frac{{(B a l P r o R u)}^{4}}{100000}$

iv) pénalité pour des écarts à 0,67 de l'efficience PDI :

$P e n E c E f P D I = 1000 x {(E f f P D I - 0,67)}^{2}$

v) pénalité pour des teneurs de la ration trop faibles en fibres apportées par les fourrages NDFFO :

$P e n E c N D F F O = e x p [- 20 \times (\frac{N D F F O % M S}{100} - 0,35)]$

Ces cinq critères, de même poids, sont additionnés au sein d'une fonction d’optimisation globale que le programme cherche à minimiser de manière à trouver la ration optimale au sein de toutes les rations a priori possibles. La figure 6 présente les traces des quatre dernières fonctions lorsqu'on les applique aux données de la base de données « Caprinut » de l'Unité MoSAR (INRA 2018) sur les données expérimentales caprines. Sur cette base de données, il apparait que seules les rations extrêmes présentent des valeurs non négligeables sur la fonction d'optimisation. Notons que les critères de pondération sont susceptibles d’évoluer en fonction du contexte et du point de vue qu’on porte sur le rationnement.

Figure 6. Valeurs des fonctions de pénalisation selon les écarts au bilan UFL nul (PenEcBilUFL, 6a), les écarts à BalProRu = 0 (PenEcBPR, 6b), les écarts d'efficience des PDI par rapport à 0,67 (PenEcEfPDI, 6c) et aux teneurs trop faibles en NDFFO des rations (PenEcNDFFO, 6d).

Save View full size Expand inline Collapse inline

3.3. Étape 3 : le calcul des réponses d’ingestion et de production des individus et des lots

a. Les calculs des réponses individuelles

La quantité de concentré MSICOCib calculée pour la cible, de composition et valeurs nutritionnelles fixées pour la couverture de ses besoins, est apportée aux autres chèvres du lot (sauf dans le cas des rations comprenant des fourrages et concentrés mélangés cf. 2.c). Ces chèvres, autres que la cible, sont donc en situation de réponse, car elles sont a priori, soit suralimentées (si PLSpot_i i > PLSpotCib), il importe donc de leur appliquer des modèles de lois de réponse. On calcule donc pour chaque chèvre autre que la cible les réponses adaptatives de l'ingestion de fourrage à l'aide de l'Eq [S4a], (Matériel Supplémentaire). On intègre ainsi pour chaque animal un phénomène de substitution entre fourrage et concentré autour de son pivot nutritionnel (BilUFLth = 0). La figure 5b montre un exemple de résultat obtenu : logiquement l'écart entre les valeurs de MSIFOPiv et MSIFO s'accroit pour les animaux dont le potentiel est plus faible, et pour ceux-ci la proportion de concentré (PCO) augmente.

Sur la figure 7a, on retrouve la réponse de l'ingestion du fourrage (Eq [S4a]) à l'accroissement de l'apport de concentré (ΔMSICO). Cette figure 7a montre également la réponse de la PLS pour les individus du lot suite aux calculs de l'Eq [S4h] qui intègre les réponses des productions de MG (RepMG, Eq [S4c]), MP (RepMP, Eq [S4d]) et ML (RepML, Eq [S4e]) aux variations de ΔMSICO. Différentes réponses peuvent être ainsi calculées à partir des valeurs individuelles de ΔMSICO. Par exemple, la figure 7b montre les différences entre les chèvres des valeurs du bilan UFL/j et de la proportion de concentré (PCO). Sur cette figure, on voit l'intérêt de l'animal faible comme sentinelle par rapport à un bilan UFL trop excédentaire et une proportion de concentré trop élevée (risque d'acidose).

Figure 7. Relations intra-lot entre les PLS potentielles et (a) les réponses de l'ingestion de fourrage et de la PLS et (b) les valeurs du bilan UFL et la proportion de concentré (PCO).

Save View full size Expand inline Collapse inline

b. Les calculs des réponses du lot

Celles-ci sont obtenues en sommant les résultats des individus. Pour un contexte donné, il est important de savoir que le choix du niveau de la cible a une influence marquée sur les niveaux d'ingestion de fourrage et de concentré d'un lot ainsi que, logiquement, sur les réponses productives. Ainsi, la figure 8 montre l'influence du critère RapCibLot sur les niveaux d'ingestion du concentré et du fourrage (figure 8a) et sur la réponse de la production laitière (figure 8b) ; pour cette exploration on a retenu une large variation de ce critère, les valeurs RapCibLot < 1 correspondent à des lots globalement sous alimentés. Pour un potentiel donné d'un lot (environ 4 kg de PLS), et une qualité moyenne de fourrage (UELFO = 1,05), l'amplitude de la variation de MSICO est d'environ 0,5 kg entre les valeurs 0,8 à 1,2 de RapCibLot. La réponse laitière à RapCibLot est positive (0,45 kg en moyenne entre les valeurs 0,8 et 1,2 de RapCibLot) et un peu meilleure si la qualité du fourrage est moins bonne, par un effet de compensation plus marqué du concentré. Notons également l'influence importante de la qualité du fourrage sur la quantité de concentré à apporter à un lot (environ 1,3 kg/j de différence moyenne entre les valeurs UELFO = 0,95 et 1,15, figure 8a). Ces résultats montrent également qu'il est possible d'avoir des valeurs RapCibLot < 1 ce qui correspond à un lot globalement sous-alimenté. A partir de ces données il est possible de calculer des critères d'efficience, par exemple un accroissement de ΔRapCibLot = 0,1 augmente le rapport MSICO/PLS d'environ 0,30 et exige donc plus de MSICO par kg de lait.

Figure 8. Influence des valeurs du critère RapCibLot sur (8a) l'ingestion de MS de concentré (rouge) et de fourrage (vert) en interaction avec la valeur UELFO du fourrage (0,95 = pointillé court ; 1,05 = pointillé long ; 1,15 = continu) et (8b) sur la réponse de la production laitière.

Save View full size Expand inline Collapse inline

4. Prévision des potentiels individuels (PLSpoti) à partir des productions observées (PLSi)

4.1. Description de la démarche globale

Il s'agit d'appliquer la démarche d'ingénierie reverse décrite à la figure 3. Cette démarche est mise en œuvre pour construire un modèle de prévision des potentiels individuels de production à partir de la production observée et du constat d’alimentation ; elle est résumée dans le diagramme de la figure 9. Cette démarche s'applique à partir de la connaissance de deux ensembles de données :

i) les données observées au niveau des individus (PL_i, TB_i, TP_i, d'où on calcule PLS_i) et des moyennes des lots : PLmoy, TBmoy, TPmoy et PLSmoy ;

ii) les estimations des potentiels du lot au niveau de la lactation (PLpot300, TBpot300 et TPpot300) puis au stade de lactation (St) considéré (PLpot, TBpot, TPpot et PLSpot). Lorsque ces valeurs ne sont pas connues, il est nécessaire d’en faire une première estimation à partir des valeurs moyennes observées pour le lot au stade considéré, cette démarche est décrite ci-dessous (cf. § 4.2 et 4.3).

Notons que dans ces démarches, on suppose que le TP du lait des chèvres n'est pas significativement influencé par l'alimentation et reste donc constant et égal à son potentiel. Cette hypothèse est conforme aux indications de Sauvant et Giger-Reverdin (2018).

4.2. Étape 1 : Estimation simple des moyennes du lot des productions potentielles laitière standard et de matière grasse (PLSpot et PMGpot)

Cette démarche correspond aux lignes pointillées bleues sur la figure 9. Pour prédire la production potentielle moyenne (PLpot), nous avons calculé les valeurs de PLmoy obtenues à partir des combinaisons factorielles des trois facteurs suivants :

i) le niveau de production potentielle moyenne du lot pour lequel nous avons considéré trois valeurs : PLpot = 3,0, 4,0 et 5,0 kg/j avec un ETPL = 0,8 kg ;

ii) la valeur d'encombrement UELFO du fourrage pour laquelle nous avons considéré également trois valeurs d’UELFO : Bon=0,95 ; Moyen=1,05 ; Médiocre=1,15 UELFO, avec un code associé CODUEF = 10 * (UELFO – 1,05)

iii) puis, à l'intérieur de chacun des 9 contextes (PLpot x CODUEF) ainsi définis, nous avons appliqué 5 niveaux de choix de la chèvre cible correspondant aux niveaux de couverture %COUV= 10 ; 30 ; 50 ; 70 ; 90 % des animaux ayant leurs besoins UFL couverts au niveau du lot. La variable codée correspondante est, comme pour la partie 3.2.a, CODPROP=(%COUV/100) – 0,5.

Avec ce dispositif de simulation, un ensemble de rations correspondant à 45 contextes a été calculé. Nous avons ensuite cherché à prédire par régression multiple la variable PLpot à partie de PLmoy et des paramètres CODPROP et CODUEF (procédure d'ingénierie reverse). La variable explicative majeure est de loin la PLmoy. La variable CODPROP joue aussi un rôle clef, seule ainsi que les deux produits d'interaction CODPROP × CODUEF et CODPROP × PLmoy. La régression obtenue de prédiction de la PLSpot du lot est assez précise :

$P L p o t = 0,0697 + 0,98831 \times P L m o y - 1,5178 \times C O D P R O P$

$- 0,1740 \times C O D P R O P \times C O D U E F$

$+ 0,1759 \times C O D P R O P \times P L m o y$
(n=45, R²=0,999, ETR=0,035) [8a]

Pour la prédiction de PMGpot la démarche est la même à partir des calculs de la moyenne observée du lot (PMGmoy) à partir des valeurs de PMGpot et des critères CODPROP et CODUEF. La régression obtenue est :

$P M G p o t = 5,75 + 0,97525 \times P M G m o y - 59,15 \times C O D P R O P$

$- 5,673 \times C O D U E F \times C O D P R O P$

$0,1975 \times C O D P R O P \times P M G m o y$ (n=45, R²=0,997, ETR=1,48) [8b]

La connaissance de taux potentiels, TBpot = PMGpot/PLpot et TPpot = TPmoyt, permet d'avoir une estimation de la PLSpot du lot (figure 9). Cette variable rentre initialement dans les boucles de calculs.

Figure 9. Diagramme décrivant le calcul des potentiels individuels PLSpoti (1) en vert : boucle des itérations pour calculer la pente BPLS (cf. ci-dessous) ; en bleu pointillé : les flèches correspondant à la prédiction directe de PLpot (cf. § 4.2).

Save View full size Expand inline Collapse inline

Les rectangles orange correspondent aux critères de contexte, les gris aux moyennes observées, les bleus aux valeurs individuelles.

4.3. Étape 2 : Calculs des valeurs individuelles des taux à partir des productions individuelles observées (PLi) et des moyennes des taux par lot

En pratique, il arrive fréquemment que les productions individuelles (PL_i) soient connues, mais que seules les valeurs moyennes du lot, TBmoy et TPmoy, soient disponibles. Dans cette situation, on suggère d'estimer les valeurs individuelles, TB_i et TP_i, en tenant compte des relations globales négatives qui existent au sein des lots entre les taux et les productions, ainsi que la relation systématique positive liant les deux taux. Donc, si on connaît les valeurs moyennes d'un lot, TBmoy et TPmoy, il est possible de s'appuyer sur des relations générales entre celles-ci et les niveaux de production laitière des individus, calculées à partir d'un vaste jeu de résultats représentatifs du contrôle laitier (Bluet, non publié). Ces relations aboutissent aux variables encadrées en bleu de la figure 9.

La relation des variations individuelles du TP lait (g/kg) en fonction de la PL est :

${T P}_{i} = 39,46 - 1,458 \times {P L}_{i}$
(n=26746, ETR=3,5) [9a]

Dans cette relation, c'est la pente de -1,458 qui est le paramètre générique. Si on est dans une situation où PLmoy et TPmoy sont connus pour le lot, on doit d'abord calculer la nouvelle constante, dépendante de TPmoy et PLmoy, puis on peut estimer les TP_i :

${T P}_{i} = T P c s t e - 1, 458 \times {P L}_{i} = (T P m o y + 1, 458 \times P L m o y) - 1, 458 \times {P L}_{i}$
[9b]

Pour le TB, on a la relation globale suivante à partir des résultats du contrôle laitier :

${T B}_{i} = 15,62 + 0,681 \times {T P}_{i} - 0,788 \times {P L}_{i}$
(n=26730, ETR=5,7) [10a]

Avec le même principe que pour le TP, on peut recalculer la constante à partir des valeurs moyennes du lot pour en déduire les valeurs TB_i des individus :

${T B}_{i} = T B c s t e + 0,681 \times {T P}_{i} - 0,788 \times {P L}_{i}$

$= (T B m o y - 0,681 \times T P m o y + 0,788 \times P L m o y)$

$+ 0,681 \times {T P}_{i} - 0,788 \times {P L}_{i}$
[10b]

On déduit ensuite, à partir des PL_i, TP_i et TB_i, les productions de lait standard individuelles à TB=35 et TP=31 g/kg (cf. Eq 21.7b, INRA 2018) :

${P L S}_{i} = \frac{P L i}{0,389} \times [0,389 + 0,0052 \times ({T B}_{i} - 35) + 0,0029 \times ({T P}_{i} - 31)]$
[11]

On peut donc en déduire la PLSmoy du lot ainsi que l'écart-type observé de cette PLS (cf. variable ETPLSobs sur la figure 9). Rappelons que cette démarche ne s'applique que si les valeurs de TB_i et TP_i ne sont pas connues.

4.4. Étape 3 : la prévision des productions potentielles individuelles PLSpoti

a. Prévision des valeurs PLSpoti à l'intérieur d'un contexte :

L'objectif est de prédire le coefficient BPLS de pente de la droite reliant les valeurs prédites PLSpot_i aux valeurs observées PLS_i. Cette droite inclue la PLS de l'animal cible (PLSCib) dont la valeur ne change pas entre l'observé et le potentiel (PLSobsCib=PLSpotCib=PLSCib) et sert de pivot de rotation à la relation (figure 10). On a donc à calculer le coefficient de pente BPLS de l'équation générique suivante pour pouvoir calculer les PLSpot_ià partir des valeurs observées PLSobs_i :

${P L S p o t}_{i} = P L S C i b + B P L S \times ({P L S o b s}_{i} - P L S C i b)$
[12]

La démarche consiste d'abord à partir de valeurs de PLSpot_i pour en déduire les PLSobs_i selon la démarche de calcul des réponses. Ensuite, on cherche à prédire les PLSpot_i à partir des PLSobs_i (<=> ingénierie reverse). Pour calculer les valeurs de la pente BPLS à travers des contextes les plus souvent rencontrés, nous avons simulé en combinaison factorielle, comme dans la partie 4.2, les 3 facteurs explicatifs suivants :

i) le niveau de production potentielle moyenne du lot pour lequel nous avons considéré trois valeurs : PLSpot = 3,0, 4,0 et 5,0 kg/j, avec ETPLS = 0,8 kg, ces 2 critères permettent d'obtenir les valeurs de PLSpot_i en supposant une distribution normale des valeurs. Le code de caractérisation du potentiel du lot pour la prévision est : CODPLSpot = (PLSpot - 4). Il prend les valeurs : -1 ; 0 ; 1 ;

ii) la valeur d'encombrement UELFO du fourrage pour laquelle nous avons considéré également trois valeurs d’UELFO : Bon=0,95 ; Moyen=1,05 ; Médiocre=1,15 UEL/kg MS, avec un code associé CODUEF = 10 * (UELFO – 1,05) dont les valeurs sont : -1 ; 0 ; 1 ;

iii) puis, à l'intérieur de chacun des 9 contextes ainsi définis, nous avons appliqué 5 niveaux de choix de la chèvre cible correspondant aux % des chèvres ayant leurs besoins UFL couverts (%COUV=10 ; 30 ; 50 ; 70 ; 90 %) et aux valeurs correspondantes du rapport RapCibLot (cf. Eq 7) avec la variable CODPROP = (%COUV/100) – 0,5 = -0,4 ; -0,2, 0,0 ; 0,2 ; 0,4.

Pour chacune de ces 45 contextes ainsi définis (3 × 3 × 5) un lot de 500 individus a été simulé. Ainsi, après avoir obtenu PLSpotCib et calculé MSICOCib (cf partie 3.3.b), nous avons calculé les réponses individuelles des 500 individus selon la démarche décrite dans les parties 3.1, 3.2 et 3.3 ainsi que les productions observées PLSobs_i. En conséquence, pour chaque contexte, nous avons pu calculer la valeur de la pente BPLS entre les valeurs de PLSpot_i prises en ordonnées et celles de PLSobs_i considérées en abscisses. La figure 10 montre un exemple de détermination par régression de BPLS, qui est égal à 1,257 pour ce contexte et la série correspondante de 500 chèvres simulées. L'ingénierie reverse consiste donc ici à prédire les valeurs de PLSpot_i à partir des PLSobs_i.

Figure 10. Exemple de régression entre les valeurs individuelles observées (PLSi) et potentielles de PLS (PLSpoti).

Save View full size Expand inline Collapse inline

Exemple d'un contexte avec PLSpot = 3,4 kg/j, ETPLSpot=1kg, UELFO = 1,05 UEL/kg MS, RapCibLot = 1,3, PLSCib = 4,4 kg/j → BPLS = 1,257.

Le coefficient 1/BPLS, appelé coefficient de réduction de l’ET (REDET), traduit la baisse de variabilité des PLS entre les valeurs potentielles et les valeurs observées. Dans l’exemple de la figure 6, avec cette pente de 1,257, on obtient une valeur REDET = 1/1,257 = 0,80, ce qui signifie que ETPLSobs = ETPLSpot × 0,8 = 1 × 0,8 = 0,8 kg alors qu'il était de 1,00 sur les données d'entrée). Cela signifie donc qu'à ce stade il convient de pouvoir boucler sur la prédiction de RapCibLot en prenant la valeur initiale de ETPLSpot = 0,8. Ce calcul correspond aux flèches vertes de la figure 9. Notons que la stabilité de la solution est atteinte rapidement.

b. Prévision des PLSpoti en fonction du contexte

L'approche précédente calculée sur 500 individus a été réalisée pour chacun des 45 contextes de manière à pouvoir aboutir à une prévision correcte de BPLS en fonction des principaux critères explicatifs considérés. Globalement, la pente BPLS diminue et se rapproche de la valeur de 1 (<=> phénotypes plus proches des génotypes) lorsque (1) la qualité du fourrage s'améliore (2) le potentiel laitier s'accroit et (3) le critère RapCibLot est plus élevé. En ajustant l'ensemble des données ainsi simulées on obtient la régression générique de prédiction de BPLS :

$B P L S = 1,7047 + 0,08771 \times C O D U E F - 0,04687 \times {C O D U E F}^{2}$

$- 0,4881 \times C O D P L S p o t + 0,0699 \times {C O D P L S p o t}^{2}$

$- 0,02435 \times C O D U E F \times C O D P L S p o t - 0,2418 \times {R a p C i b L o t}^{2}$

$+ 0,2758 \times C O D P L S p o t \times R a p C i b L o t (n = 45, R^{2} = 0,98, E T R = 0,030) [13]$

Il y a donc des réponses curvilinéaires pour les 3 critères, ainsi que des interactions entre d'une part, les critères CODUEF et CODPLS, et d'autre part, CODPLSpot et RapCibLot. A ce stade, on peut donc calculer les valeurs de PLSpoti selon l’équation [12], en fonction de PLSi, PLSCib et de BPLS estimé par l’équation [13].

c. Détermination des valeurs PLpoti et PMGpoti correspondantes à PLSpoti

La notion de cible, associée à la couverture des besoins UFL potentiels, ne s'applique qu'aux valeurs de PLS. Par contre, une fois connue la PLSCib on peut calculer, grâce à la connaissance de TBCib et TPCib, une valeur correspondante de PL qu'on appelle PLCib.

$P L C i b = \frac{0,389 \times P L S C i b}{0,389 + 0,0052 \times (T B C i b - 35) + 0,0029 \times (T P C i b - 31)}$
[14]

En fait, un calcul itératif doit être appliqué entre l'équation [14] ci-dessus et les deux équations suivantes (Eq [14’] et [14’’], reliant TPCib, TBCib et PLCib :

$T P C i b = T P m o y + 1, 458 \times P L m o y - 1, 458 \times P L C i b$
[14']

$T B C i b = (T B m o y - 0, 681 \times T P m o y + 0, 788 \times P L m o y)$

$+ 0, 681 \times T P C i b - 0, 788 \times P L C i b$
[14'']

Si on n’a pas de valeurs de TBCib et TPCib, on peut estimer PLCib en appliquant une régression globale issue de données simulées, cependant cette relation est peu précise :

$P L C i b = - 0,5359 + 1,06843 \times P L S C i b$
(n=45, R²=0,99, ETR=0,053) [15]

La relation générale de calcul des valeurs de PLpoti est :

${P L p o t}_{i} = P L C i b + B P L \times ({P L o b s}_{i} - P L C i b)$
[16]

En fait, la pente de PL (BPL) est très liée à celle de BPLS, elle peut donc être prédite avec précision à partir de BPLS et du potentiel de production quantifié par la variable CODPLSpot décrite plus haut :

$B P L = - 0, 0310 + 1, 0183 \times B P L S - 0, 01904 \times C O D P L S p o t$
(n=45, R²=0,99, ETR=0,027) [17]

On peut alors appliquer une équation comparable à l'Eq [12] pour calculer la PLpotmoy au stade considéré en fonction de la PL moyenne observée (PLobsmoy) :

$P L p o t m o y = P L C i b + B P L \times (P L o b s m o y - P L C i b)$
[18]

On peut appliquer la même approche pour PMG en profitant de la même boucle de calculs et en calculant à chaque itération :

$P M G C i b = P L B C i b \times T B C i b$
[19]

et l'équation générique de prévision de PMGpoti est donc par analogie avec les Eq [12] et [18] :

${P M G p o t}_{i} = P M G C i b + B P M G \times ({P M G o b s}_{i} - P M G C i b)$
[20]

Le coefficient de pente BPMG est très lié à BPLS et peut être prédit par l'équation suivante :

$B P M G = 0,0326 + 0,9751 \times B P L S - 0,01936 \times C O D U E F$

$+ 0,01178 \times C O D P L S p o t - 0,02343$

${\times C O D P L S p o t}^{2}$
(n=45, R²=0,99, ETR=0,018) [21]

Ces différentes équations calculées permettent donc de prédire avec un degré de précision assez satisfaisant les potentiels individuels des animaux (PLSpoti, PLpoti et PMGpoti) à partir de leurs productions observées (PLSi, PL_i et PMG_i) et du contexte considéré.

5. Mise en œuvre des phases de calculs en fonction du mode appliqué dans les élevages

Sur le terrain, les étapes de calcul décrites plus haut sont mises en œuvre à travers deux principales démarches possibles, que l’on appelle mode « calcul » et mode « constat ».

5.1. Les modes « calculs »

Dans le mode « calcul », les quantités de concentrés sont fixées par l’utilisateur (avec l’objectif de nourrir l’animal cible à son potentiel) et les quantités de fourrages ingérées par chaque animal sont calculées (pour saturer la capacité d’ingestion de chaque individu). Des quantités de fourrages ingérées calculées pour chaque individu sont déduites les quantités ingérées par le lot. Ce mode consiste à appliquer les étapes décrites dans la partie 3 de cet article (calcul des niveaux d’ingestions pour les pivots individuels, partie 3.1, puis choix de la cible, partie 3.2, puis calcul des réponses, partie 3.3). Ces calculs permettent de calculer au passage les bilans nutritifs (UFL, PDI, Ca, P...) de tous les individus, puis de la moyenne du lot. Cette démarche est appliquée à partir de l'estimation a priori, ou du calcul selon la partie 4, des potentiels individuels. Ce mode est appliqué dans des situations où l’on cherche à explorer des rations possibles au sein d'un contexte donné, par exemple en faisant varier le paramètre RapCibLot pour en évaluer les conséquences.

Le mode « calcul optimisé » est comparable au précédent, sauf qu’on cherche à déterminer pour un ou deux concentrés les quantités optimales pour nourrir l’animal cible à son potentiel. Ainsi dans cette démarche, les quantités de fourrages et de concentrés seront déterminées par le calcul pour la chèvre cible avec la fonction d'optimisation décrite dans la partie 3.2.c, de manière à s'assurer que tous ses besoins nutritifs sont satisfaits.

5.2. Le mode « constat »

Dans le mode « constat », évoqué au 1.3, les quantités d’aliment ingérées et du lait produit par le lot sont constatées par l’utilisateur. On cherche ainsi à déduire les quantités ingérées par chaque individu telles que la somme des quantités ingérées par les individus soit égale aux quantités constatées. Ce mode, qui pourrait s'appeler aussi « diagnostic », consiste donc à étudier une ration constatée sur le terrain pour un lot. On connait alors les ingestions constatées, MSIFOConst et MSICOConst, et la production moyenne observée du lot considéré. Les valeurs UFL et UEL de ces aliments sont également calculées en tenant compte des interactions digestives. Dans cette approche en mode « constat », on dispose également d'une connaissance a priori de la proportion des individus dont les besoins UFL sont couverts par la cible.

Le calcul en mode « constat » est conduit en 4 étapes successives, résumées dans la figure 11 :

i) La première étape correspond au calcul des productions individuelles potentielles (PLSpot_i) d'un lot virtuel de 500 chèvres dont on connait le potentiel moyen (PLpot) et son écart-type (ETPLpot). Ce calcul est effectué sous l'hypothèse d'une loi de Gauss de distribution des PLpot_i sachant que (1) les éventuelles valeurs négatives sont supprimées et (2) les « queues de distribution » au-delà des PLpot ± 2,25 ETPLpot sont supprimées. En effet, la distribution des productions laitières des chèvres ne suit pas précisément une loi normale en raison de « queues de distribution » plus réduites. Les nombres d'animaux ainsi éliminés sont indiqués, ils ne doivent pas excéder 10 % des observations selon nos différents essais. Le calcul se poursuit pour obtenir les valeurs PLSpot_i sur la base de la connaissance des TBpot_i et TPpot_i qui sont connus ou bien estimés avec les calculs présentés dans la partie 4.3.

ii) une fois les PLSpot_i connues, on peut calculer les pivots individuels (MSICOPiv_i et MSIFOPiv_i) selon la démarche de la partie 3.1 avec le système des Eq [3] et [3']. Pour chaque individu, on tient compte dans la boucle calculatoire (1) des interactions digestives, (2) du niveau du tri avec la variable CODTRI, selon l'encadré n°2, (3) des quelques cas où MSICOPiv_i ≤ 0, dans ce cas on fixe MSICOPiv_i = 0 et MSIFOPiv_i = MSIFOMaxT_i = CI_i/UELFO et (4) des quelques cas où MSIFOPiv_i < 0,1 kg seuil minimal en dessous duquel seule l'Eq [3] relative aux UFL est appliquée pour calculer MSICO. Les nombres de cas correspondant aux situations (3) et (4) ne devrait pas excéder environ 10 % des données selon nos observations.

iii) ensuite, pour calculer les réponses ingestives et productives, le niveau d'apport de concentré apporté à tous les animaux n'est pas celui de la cible, comme dans la partie 3.2, mais celui qui est constaté sur le terrain (MSICOConst). À partir de cette donnée, on calcule les réponses des individus selon la démarche décrite en partie 3.3 en appliquant les équations de réponses [S4a] à [S4h] (cf. Matériel supplémentaire) avec ΔMSICO_i = MSICOConst - MSICOPivi. Rappelons que, pour les quelques situations avec un pivot défini avec MSICOPiv = 0 (cf. partie 3.1.c), ce sont les équations [S2a] à [S2f] qui sont appliquées pour obtenir les réponses d'ingestion de MSIFO et les réponses productives.

iv) Sauf exception, on a en général MSIFOAtt ≠ MSIFOConst. Il est donc nécessaire de mettre en œuvre une nouvelle démarche itérative pour rapprocher ces deux valeurs (figure 11). En résumé, cette démarche consiste à moduler par étape la valeur de la CI des animaux du lot dans le sens qui permet de réduire l'écart entre MSIFOAtt attendue et MSIFOConst. Pour cela, à chaque étape n, on calcule la différence relative :

${Δ M S I F O}_{n} = \frac{(M S I F O C o n s t - {M S I f o F O A t t}_{n})}{M S I F O C o n s t}$
[22]

On en déduit la relation qui va permettre de moduler la valeur de la CI à la boucle suivante n+1 :

${Δ I m p a c t C I}_{n} = 1 + 0,2 \times {Δ M S I F O}_{n}$
[22']

Le coefficient 0,2 peut être accru (à 0,5 par exemple) pour accélérer la convergence. On en déduit :

${C I}_{n + 1} = {Δ I m p a c t C I}_{n} \times {C I}_{n}$
[22"]

Une fois la CI_n+1 ainsi déterminée, on l'utilise pour boucler sur (1) les étapes de calcul des pivots individuels (partie 3.1) puis sur (2) les réponses ingestives et productives des individus, en fixant toujours l'apport de concentré à MSICOConst. A partir de là, on calcule l'étape calculatoire suivante, à partir de ΔMSIFO_n+1 = (MSIFOConst - MSIFOAtt_n+1) / MSIFOConst etc. Selon nos observations, les données convergent en général assez rapidement vers la valeur MSIFOAtt ~ MSIFOConst.

À ce stade ultime, il importe de calculer les niveaux de production prédits sur la base des niveaux d'ingestion constatés, MSIFOConst et MSICOConst. Si l'écart entre les productions moyennes prédite et constatée est important (plus de 10 %) il doit interpeller et être interprété en revisitant les différentes valeurs d'ingestion et de refus constatées, ainsi que les valeurs alimentaires des aliments, du fourrage en particulier.

À ce stade, il est aussi nécessaire de calculer le BilanUFLth moyen du lot ainsi que celui de l'animal faible. Il importe également de connaitre la position de l'animal cible a posteriori pour lequel on a BilanUFLth = 0, et d'en déduire la proportion des animaux ayant des besoins UFL couverts par cette cible a posteriori pour la comparer à la cible a priori évoquée plus haut. Toutes ces informations permettent d'effectuer un diagnostic de la situation constatée.

Cette démarche a été développée sur le logiciel Minitab version 18, puis Excel, avant d'être codée dans le logiciel Rumin’Al.

Discussion et conclusions

Les démarches proposées dans cette publication n'ont, à notre connaissance, jamais été décrites dans la littérature. La réponse de production d'un lot ne peut pas être calculée simplement comme celle d'un animal moyen multipliée par le nombre d'animaux. En effet, le choix de l'animal cible, dont les besoins sont couverts, constitue une règle qui implique des situations de réponses hétérogènes au sein de l'ensemble des animaux et induit ainsi une propriété émergente de la réponse du lot qu'il était nécessaire d'appréhender. Le modèle de lot qui sous-tend les démarches montre que, malgré la relative simplicité apparente de la problématique, le changement d'échelle de l'individu au lot est assez compliqué à résoudre si on veut traduire assez fidèlement les lois biologiques et les règles techniques qui s'appliquent. La démarche proposée est appliquée aux chèvres, cependant elle est a priori applicable à l'alimentation en lots des ovins (Bocquier et al., 1995) ou des bovins (Moulin et al., 2001), pour lesquels on veut raisonner au mieux l'apport de concentré, ressource la plus coûteuse de la ration. Par ailleurs, ce modèle se place dans la lignée des modèles « individus-centrés » intégrables dans des problématiques plus larges. De plus, ce modèle individus-lot peut être utilisé comme base pour l'établissement d'un modèle de troupeau en intégrant d'autres règles (stratégies de constitution des lots, gestion de la reproduction…).

La construction de cette démarche s'est appuyée sur la combinaison de modèles individuels basés sur des données expérimentales (INRA, 2018) et d'approches par simulation et ingénierie reverse fondées elles-mêmes sur ces modèles. La mise en œuvre de la démarche proposée nécessite l'application de plusieurs phases de calculs itératifs qui, selon les tests effectués, convergent assez rapidement ce qui permet de ne pas ralentir le processus de travail.

Les différentes démarches décrites dans ce texte permettent aux techniciens et éleveurs de disposer d'un outil original permettant de gérer au mieux l'alimentation des lots de chèvres en production, en particulier en tenant compte des réponses productives des différents individus. Pour aider à appréhender la situation alimentaire d'un lot, il est proposé de considérer non seulement la chèvre cible et la chèvre moyenne mais également la chèvre faible productrice qui sert a priori de sentinelle par rapport à des situations nutritionnelles à risque par excès. Une des originalités de ce travail concerne la proposition d'estimation des potentiels laitiers individuels des animaux à partir des valeurs observées des productions et de la qualité des fourrages distribués. Le travail a été conduit principalement sur des situations de lots conduits à l'auge, cependant les principes appliqués peuvent peut-être s'adapter à une situation de pâturage, par exemple à travers l'apport de fourrage en quantité fixe s'il s'agit d'un pâturage contraint. Dans le cas d'un pâturage non contraint avec un fourrage ad libitum, notre modèle peut être appliqué ; par exemple, il permet de retrouver assez fidèlement les résultats observés par Caillat et al. (2018) en situation de pâturage non contraint (plus de 3 kg de MS offerte/chèvre et 10h de temps d'accès).

Le choix du placement de la cible en fonction de la proportion des besoins énergétiques couverts constitue un levier de gestion du lot extrêmement important par rapport aux réponses de production attendues et surtout par rapport aux quantités d'aliments concentrés utilisées et sans doute également aux résultats économiques des élevages. Ce travail confirme le rôle important de la qualité du fourrage vis à vis des réponses et de l'ingestion de concentré, en particulier sa valeur d'encombrement et sa teneur en énergie. Enfin, pour s'adapter à la diversité des situations rencontrées sur le terrain, nous avons proposé différents modes d'application des démarches avec i) le mode « calcul » qui permet de concevoir un régime adapté à un lot et un contexte donné, et ii) le mode « constat » qui permet d'aboutir à un diagnostic précis de la cohérence des données d'ingestion et de production estimées/mesurées dans un élevage.

Ce travail n'a pas abordé la question de la comparaison entre l'alimentation en lots telle qu'elle est décrite et une alimentation ajustée individuellement par une distribution automatique et programmée des aliments concentrés (ce qui correspond au scénario de la partie 3.1). En brebis laitières, Hassoun et al. (2018) ont montré que cette technique pouvait permettre une économie d'aliments concentrés sans altération notable des performances laitières. Ce résultat est assez conforme à nos simulations car, à l'inverse, la prise en compte d'une cible au-dessus de la moyenne accroit l'ingestion du concentré mais ne modifie pas de façon importante la réponse de la production de lait qui est tamponnée par les réserves.

Enfin, ce travail conçu et réalisé au sein d'un dialogue fructueux entre représentants de la recherche, du développement et de la formation apporte une indéniable valeur ajoutée au modèle chèvre ‘individu-centré’ du système INRA 2018. Les aspects touchant aux évolutions temporelles des différents critères ont été volontairement laissés de côté, car ils seront l'objet de l'article suivant en cours de rédaction.

Remerciements

Les auteurs tiennent à remercier Pierre Nozière (INRAE) pour la relecture particulièrement attentive du manuscrit et pour ses suggestions afin d’en faciliter la compréhension de la lecture. Ils remercient également Julien Charvet (Okteo) pour sa persévérance à coder le logiciel Rumin’Al à partir d'informations techniques qui ne sont pas de son monde.

Matériel supplémentaire

Actualisation des réponses aux apports de concentré

S1. Actualisation des réponses aux apports de concentré à partir des situations de pivot nutritionnel (BilUFLth = 0)

Une fois que la ration de chaque individu au pivot nutritionnel a été calculée (voir partie 3.1.a) et que l'apport de concentré MSICOCib à la cible a été déterminé (voir partie 3.1.d), il est possible de calculer pour chaque chèvre l'écart de MSICO entre MSICOCib appliqué à toutes les chèvres du lot et sa valeur pivot :

$M S I C O = M S I C O C i b - M S I C O P i v$
[S3]

Sur la base de ce critère ΔMSICO, on calcule les différentes réponses individuelles d’ingestion et de production qui actualisent des équations proposées préalablement (INRA, 2018), pour le fourrage ingéré on a (figure Sb) :

$R e p M S I F O = (1, 56) - 0, 70 \times M S I C O - 0, 066 \times {M S I C O}^{2}$
[S4a]

- pour la réponse de la production de lait PL brute en kg/j (Eq 21.52, INRA, 2018 ; actualisée) :

$R e p P L = 0, 89 \times Δ M S I C O - 0, 211 \times {Δ M S I C O}^{2}$
[S4b]

- pour la réponse de la production des matières grasses en g/j (cf. tableau 21.9, INRA, 2018 ; actualisé) :

$R e p M G = 32, 2 \times Δ M S I C O - 10, 47 \times {Δ M S I C O}^{2}$
[S4c]

- pour la réponse de la production des protéines en g/j (cf. tableau 21.9, INRA, 2018 ; actualisé) :

$R e p M P = 27, 0 \times Δ M S I C O - 7, 55 \times {Δ M S I C O}^{2}$
[S4d]

- pour réponse de la production du lactose en g/j, en supposant, faute de données en nombre suffisant, que la teneur en lactose du lait reste constante :

$R e p L a c t = 45 \times R e p P L$
[S4e]

Les nouveaux taux se calculent alors par les rapports suivants (en g/kg) :

$T B = \frac{(M G P i v + R e p M G)}{(P L P i v + R e p P L)}$
[S4f]

$T P = \frac{(M P P i v + R e p M P)}{(P L P i v + R e p P L)}$
[S4g]

On peut en déduire par calcul les réponses des TB et TP. Notons également qu'il existe une équation spécifique pour RepTB (Tab 21.9, INRA, 2018). La réponse de la PLS se calcule ensuite de façon équivalente à l’équation S2f :

$R e p P L S = (\frac{1}{0,389}) \times (\frac{9,39 \times R e p M G + 5,47 \times R e p M P + 3,95 \times R e p L a c t}{1760})$
[S4h]

S2 Actualisation des réponses aux apports de concentré pour la situation MSICOPiv=0

La régression intra-expérience actualisée de l'ingestion des fourrages (MSIFO, kg/j) en fonction de l'apport de concentré en kg/j (MSICOCib en mode calcul ou MSICOConst en mode constat) est (figure S) :

$M S I F O = 1,86 - 0,57 M S I C O - 0,088 {M S I C O}^{2}$
(nexp=45, n=126, ETR=0,18) [S1a]

Les 45 expériences considérées étaient toutes focalisées sur l'effet d'une variation de l'apport de concentré. La constante 1,86 de cette équation est le rapport CI/UELFO moyen des expériences prises en compte. Pour un animal donné, caractérisé par sa CI, cette ordonnée à l'origine varie donc en fonction de UELFO, la valeur d'encombrement du fourrage proposée dans les tables INRA 2018. On peut déduire de l'équation [S1a] la relation moyenne intra de prévision de la substitution marginale, TSm, qui varie de 0,57 à 0,92 au sein du jeu des données considérées :

$T S m = - (\frac{d M S O f o}{d M S I C O}) = 0,57 + 0,176 \times M S I C O$
[S1b]

On en déduit, par intégration, le taux de substitution global TSg, calculé pour une ration donnée à partir de la valeur de MSICO = 0, il varie de 0,57 à 0,75 au sein des données considérées selon la relation :

$T S g = 0, 57 + 0, 088 \times M S I C O$
[S1c]

La réponse de MSIFO en kg MS/j (Eq 21.51, INRA 2018, actualisée) pour la situation MSICOPiv=0 correspond donc à l'application de l'équation [S1a] sans la constante.

$R e p M S I F O = - 0, 57 \times M S I C O - 0, 088 \times {M S I C O}^{2}$
[S2a]

Il en est de même pour les réponses de production pour lesquelles les équations ont aussi été actualisées ; pour les productions les réponses ne tiennent pas compte de la constante, qui est indiquée pour mémoire entre parenthèses :

$R e p P L M S I C O = (1,953) + 1,330 \times M S I C O - 0,323 \times {M S I C O}^{2}$
(n=116, nexp=40, ETR=0,30) [S2b]

Pour la réponse de la production de matières grasses :

$R e p M G M S I C O = (61,52) + 59,23 \times M S I C O - 19,30 \times M S I C O^{2}$
(n=115, nexp=40, ETR=11,9) [S2c]

Pour la réponse de la production de protéines :

$R e p M P M S I C O = (58,37) + 43,16 \times M S I C O - 12,30 \times M S I C O^{2}$
(n=115, nexp=40, ETR=9,2) [S2d]

Pour la réponse de la production de lactose en supposant que sa teneur est constante et égale à 45 g/kg lait :

$R e p M L M S I C O = (92,25) + 64,24 \times M S I C O - 17,42 \times M S I C O^{2}$
(n=116, nexp=40, ETR=13,7) [S2e]

Donc, pour la réponse de la production de lait standard on a :

$R e p P L S = (\frac{1}{0,389}) \times (\frac{(9,39 \times R e p M G + 5,47 \times R e p M P + 3,95 \times R e p L a c t)}{1760})$
[S2f]

Figure S. Réponses actualisées de l'ingestion de fourrage (MSIFO) aux apports de concentré (a) à partir de MSICO=0 (cf. Eq S1a) et (b) à partir de ΔMSICO = 0 (cf. Eq S4a).

Save View full size Expand inline Collapse inline

Références

Bocquier F., Caja G., 2001. Production et composition du lait de brebis : effets de l'alimentation INRA Prod. Anim., 14, 129-140. doi:10.20870/productions-animales.2001.14.2.3734
Bocquier F., Guillouet P., Barillet F., 1995. Alimentation hivernale des brebis laitières : intérêt de la mise en lots. INRA Prod. Anim., 8, 19-28. doi:10.20870/productions-animales.1995.8.1.4101
Caillat H., Charpentier A., Ranger B., Bruneteau E., Boisseau C., Delagarde R., 2018. Variabilité inter-individuelle de l’ingestion d’herbe par des chèvres laitières au pâturage. In : Renc. Rech. Rum., INRA - Institut de l'Élevage (Eds). 24, 170.
Hassoun P., Hardy A., De Boissieu C., Tesniere A., Legarto J., 2018. Effets d’un apport de concentré ajusté aux besoins individuels comparés à un apport unique à des brebis laitières Lacaune alimentées à base de foin ou d’ensilage. Renc. Rech. Rum., INRA - Institut de l'Élevage (Eds). 24, 139-143.
Idele, 2011. L'alimentation pratique des chèvres laitières. Technipel. 216p.
INRA, 2007. Alimentation des bovins, ovins et caprins. Besoin des animaux - Valeurs des aliments. Éditions Quae, Versailles, France, 307p.
INRA, 2018. Alimentation des ruminants. Éditions Quae, Versailles, France, 728p.
Moulin C., Girard N., Dedieu B., 2001. L'apport de l'analyse fonctionnelle des systèmes d'alimentation. Fourrages, 167, 337-363.
Sauvant D., Bluet B., 2020. Extension spatio-temporelle du modèle chèvre INRA 2018 à l’alimentation par lot et au cours du cycle de production. Renc. Rech. Rum., INRA - Institut de l'Élevage (Eds). 25, 346-349.
Sauvant D., Giger-Reverdin S., 2018. 21. Caprins en lactation et en croissance. In : Alimentation des ruminants. Éditions Quae, Versailles, France, 399-441.
Sauvant D., Puillet L, Bluet B., 2021, Extension spatio-temporelle du modèle chèvre INRA 2018 (2) l'évolution de la dynamique des réserves, du poids vif et de la NEC sur un cycle productif. INRAE Prod. Anim. (soumis).

Résumé

Cette publication présente une démarche visant à aider à la gestion alimentaire des lots de chèvres laitières en s'appuyant sur le modèle individuel « chèvre » proposé par INRAE (INRA, 2018). Cette démarche consiste à s'appuyer sur des paramètres de la gestion des lots, en particulier sur le choix de l'animal cible qui est nourri à son potentiel. Ce choix permet i) de prédire les potentiels de production de chaque animal du lot en fonction des productions moyennes observées pour le lot et de la qualité des fourrages distribués, et ii) de prédire les réponses du lot en matière d'ingestion de concentrés et de fourrages, ainsi que de production de lait et de bilan nutritionnel, Outre l'animal cible, la chèvre moyenne, représentative de l'ensemble du lot, et la chèvre faible productrice, utilisée comme sentinelle pour des rations à risque, sont systématiquement prises en compte. Les démarches proposées sont applicables à différents contextes d'élevage. En particulier, elles peuvent être mises en œuvre pour établir une ration a priori ou bien pour analyser une ration constatée sur le terrain.

Auteurs

Daniel SAUVANT

daniel.sauvant@agroparistech.fr

Affiliation : 1Université Paris-Saclay, INRAE, AgroParisTech, UMR Modélisation Systémique Appliquée aux Ruminants (MoSAR), 75005, Paris, France

Pays : France

Patrick CHAPOUTOT

Affiliation : Université Paris-Saclay, INRAE, AgroParisTech, UMR Modélisation Systémique Appliquée aux Ruminants (MoSAR), 75005, Paris, France

Pays : France

Sylvie GIGER-REVERDIN

Affiliation : 1Université Paris-Saclay, INRAE, AgroParisTech, UMR Modélisation Systémique Appliquée aux Ruminants (MoSAR), 75005, Paris, France

Pays : France

Bertrand BLUET

Affiliation : Institut de l’Élevage, CS 45002, F-86550, Mignaloux-Beauvoir, France

Pays : France

Pièces jointes

Pas d'informations justificatives pour cet article

##plugins.generic.statArticle.title##

Vues: 1483

Téléchargements

PDF: 255

XML: 144

Chapeau

Introduction

1. La problématique de l'alimentation en lots

1.1. Définition du lot alimentaire et des animaux repères

1.2. Les démarches appliquées

1.3. Les informations connues a priori

2. Rappels et actualisations des principales équations de base

2.1. Rappels sur la prévision de la capacité d'ingestion et des besoins énergétiques individuels.

2.2. Actualisation des équations de prévision des réponses individuelles aux apports alimentaires

a. Influences des niveaux offerts et des apports de concentré

b. Les réponses aux apports d'aliment concentré ou de nutriments à partir des situations de pivot nutritionnel BilUFLth = 0

c. Cas particulier des rations comprenant des fourrages et concentrés mélangés

3. Modélisation des réponses des lots à partir des potentiels individuels

3.1. Étape 1 : le calcul des rations individuelles équilibrées au « pivot nutritionnel »

a. Principes de base du calcul

b. La prise en compte des modifications de la capacité d'ingestion et des valeurs alimentaires

c. Cas particuliers des situations de solutions impossibles du système des équations [3] et [3']

3.2. Étape 2 : le repérage de la chèvre cible et le calcul de sa ration

a. Prévision de la PLS potentielle de la « chèvre cible »

b. Détermination de l'apport de concentré à la chèvre cible

c. Optimisation du calcul de la ration de la chèvre cible

3.3. Étape 3 : le calcul des réponses d’ingestion et de production des individus et des lots

a. Les calculs des réponses individuelles

b. Les calculs des réponses du lot

4. Prévision des potentiels individuels (PLSpoti) à partir des productions observées (PLSi)

4.1. Description de la démarche globale

4.2. Étape 1 : Estimation simple des moyennes du lot des productions potentielles laitière standard et de matière grasse (PLSpot et PMGpot)

4.3. Étape 2 : Calculs des valeurs individuelles des taux à partir des productions individuelles observées (PLi) et des moyennes des taux par lot

4.4. Étape 3 : la prévision des productions potentielles individuelles PLSpoti

a. Prévision des valeurs PLSpoti à l'intérieur d'un contexte :

b. Prévision des PLSpoti en fonction du contexte

c. Détermination des valeurs PLpoti et PMGpoti correspondantes à PLSpoti

5. Mise en œuvre des phases de calculs en fonction du mode appliqué dans les élevages

5.1. Les modes « calculs »

5.2. Le mode « constat »

Discussion et conclusions

Remerciements

Matériel supplémentaire

Actualisation des réponses aux apports de concentré

S1. Actualisation des réponses aux apports de concentré à partir des situations de pivot nutritionnel (BilUFLth = 0)

S2 Actualisation des réponses aux apports de concentré pour la situation MSICOPiv=0

Références

Résumé

Auteurs

Daniel SAUVANT

Patrick CHAPOUTOT

Sylvie GIGER-REVERDIN

Bertrand BLUET

Pièces jointes

##plugins.generic.statArticle.title##

Articles les plus lus par le même auteur ou la même autrice